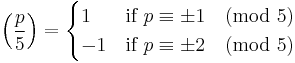Wall–Sun–Sun prime

Unsolved problems in mathematics
Are there any Wall–Sun–Sun primes?

In number theory, a Wall–Sun–Sun prime or Fibonacci–Wieferich prime is a certain kind of prime number which is conjectured to exist although none are known.

Contents

Definition

A prime p > 5 is called a Wall–Sun–Sun prime if p2 divides the Fibonacci number 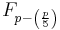F_{p - \left(\frac{{p}}{{5}}\right)}, where the Legendre symbol 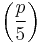\left(\frac{{p}}{{5}}\right) is defined as

\left(\frac{p}{5}\right) = \begin{cases} 1 &\text{if }p \equiv \pm1 \pmod 5\\ -1 &\text{if }p \equiv \pm2 \pmod 5 \end{cases}

Existence

It has been conjectured that there are infinitely many Wall–Sun–Sun primes.[1] No Wall–Sun–Sun primes are known as of October 2011.

In 2007, Richard J. McIntosh and Eric L. Roettger showed that if any exist, they must be > 2×1014.[2] Dorais and Klyve extended this range to 9.7×1014 without finding such a prime.[3]

History

Wall–Sun–Sun primes are named after D. D. Wall,[4] Zhi Hong Sun and Zhi Wei Sun; Z. H. Sun and Z. W. Sun showed in 1992 that if the first case of Fermat's last theorem was false for a certain prime p, then p would have to be a Wall–Sun–Sun prime.[5] As a result, prior to Andrew Wiles' proof of Fermat's last theorem, the search for Wall–Sun–Sun primes was also the search for a counterexample to this centuries-old conjecture.

See also

References

  1. ^ Klaška, Jiří (2007), "Short remark on Fibonacci−Wieferich primes", Acta Mathematica Universitatis Ostraviensis 15 (1): 21–25, http://dml.cz/dmlcz/137492 .
  2. ^ McIntosh, R. J.; Roettger, E. L. (2007). "A search for Fibonacci−Wieferich and Wolstenholme primes". Mathematics of Computation 76 (260): 2087–2094. doi:10.1090/S0025-5718-07-01955-2. http://docs.google.com/viewer?a=v&q=cache:vR220ldvztoJ:citeseerx.ist.psu.edu/viewdoc/download%3Fdoi%3D10.1.1.105.9393%26rep%3Drep1%26type%3Dpdf+wolstenholme+prime+fermats+last+theorem&hl=de&gl=de&pid=bl&srcid=ADGEESirfd2SXu_6m_rBnSa9_J1FEV6pXYhaszGMjogRPDIU003Qu8eBknikKaTgUzQpx2vBJE8zxyIyu8c5bo_UgXpGYXP2PeSvMaXSqUrynptDXRktVJw28_i2Tm6GCdEtYWOt7e7E&sig=AHIEtbQRB1Z0Tpz9k0f8kYnzyJp1saeAPg. 
  3. ^ Dorais, F. G.; Klyve, D. W. (2010). Near Wieferich primes up to 6.7 × 1015. http://www-personal.umich.edu/~dorais/docs/wieferich.pdf. 
  4. ^ Wall, D. D. (1960), "Fibonacci Series Modulo m", American Mathematical Monthly 67 (6): 525–532, doi:10.2307/2309169 
  5. ^ Sun, Zhi-Hong; Sun, Zhi-Wei (1992), "Fibonacci numbers and Fermat’s last theorem", Acta Arithmetica 60 (4): 371–388, http://matwbn.icm.edu.pl/ksiazki/aa/aa60/aa6046.pdf 

Further reading

External links